Secure State Estimation against Sparse Attacks on a Time-varying Set of Sensors

Zishuo Li, Muhammad Umar B. Niazi, Changxin Liu, Yilin Mo, Karl H. Johansson

Department of Automation, Tsinghua University, Beijing, China

Division of Decision and Control Systems, Digital Futures, School of EECS, KTH, Stockholm, Sweden

Laboratory for Information and Decision Systems, Massachusetts Institute of Technology, Cambridge, USA

BACKGROUND: Security Problem of Estimation

Safety Critical Industries

  • High safety requirements.
  • More vulnerable System
    • Modern control systems are becoming more open to the cyber-world.
    • More complex threats on estimation algorithms.

Resilient Estimation against sparse attack

$p$ sparse attack: The corrupted sensor set $\mathcal{C}$ satisfies $|\mathcal{C}| \leq p,\ \forall k$.

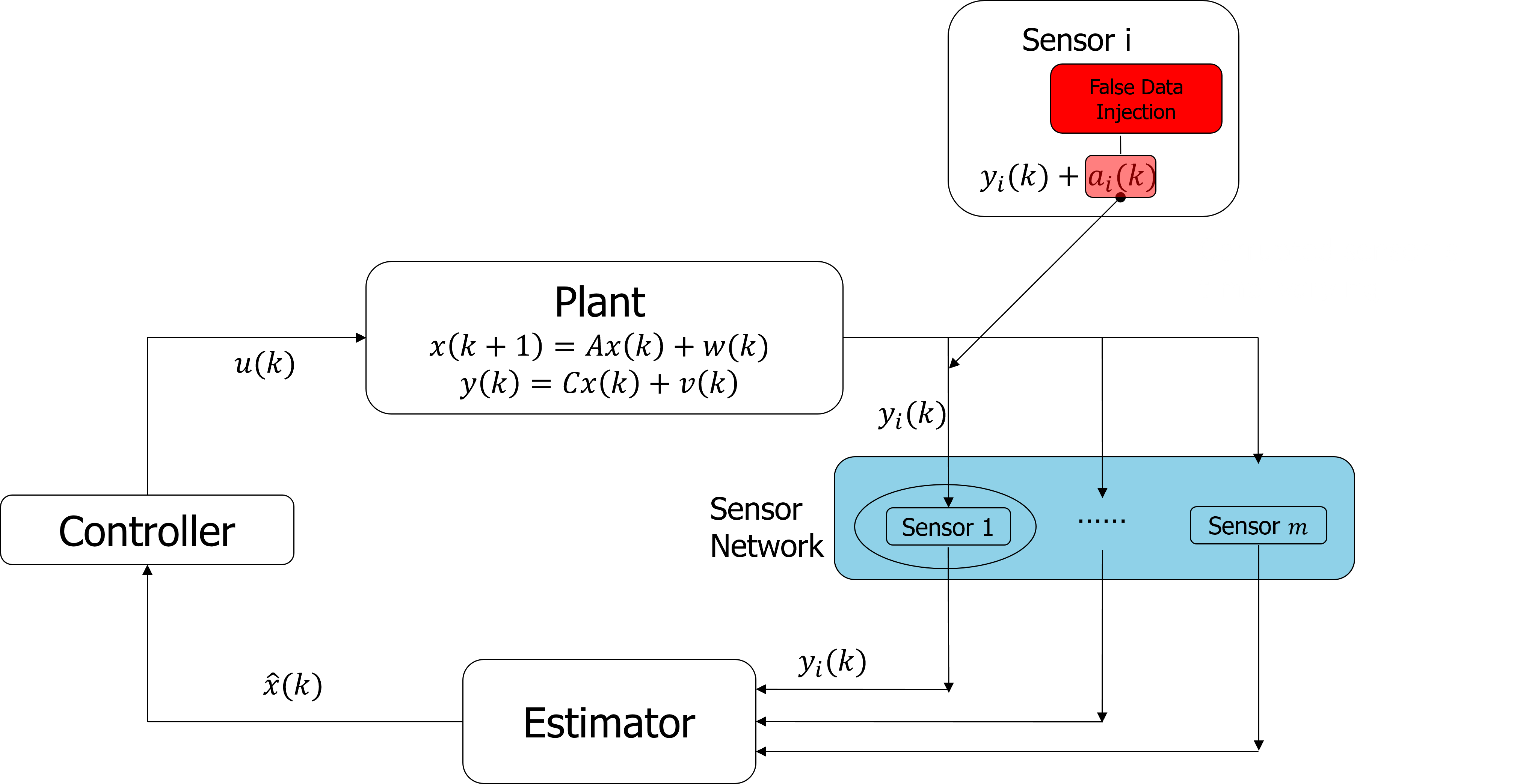
Figure

Resilient Estimation against time-varying sparse attack

Time-varying $p$ sparse attack: The corrupted sensor set $\mathcal{C}(k)$ satisfies $|\mathcal{C}(k)| \leq p,\ \forall k$.

Figure

Problem Formulation

  • System equation and measurement equation:

    $$ x(k+1)=Ax(k)+w(k), $$

    $$ y(k)=Cx(k)+v(k)+a(k), $$

    • where $x(k)\in{\color{var(--myred)}{\mathbb{R}^n}}$, and

    $$ y(k)\triangleq \begin{bmatrix} y_1(k)\\ \vdots\\ y_m(k) \end{bmatrix}\in {\color{var(--myred)}\mathbb{R}^m}, C\triangleq \begin{bmatrix} C_1\\ \vdots\\ C_m \end{bmatrix}, a(k)\triangleq \begin{bmatrix} a_1(k)\\ \vdots\\ a_m(k) \end{bmatrix} $$

  • Measurement equation of sensor $i$:

    $$ y_i(k)=C_ix(k)+v_i(k)+a_i(k). $$

  • process noise $w(k)$ and measurement noise $v(k)$ are bounded: $\|w(k)\|_2\leq\mathcal{B}_w $, $\|v(k)\|_2\leq\mathcal{B}_v $.
  • $(A,C)$ is observable. Note that $(A, C_i)$ is not necessarily observable.
  • Target : $\|\hat{x}(k)-x(k)\|\leq \text{Constant}$ for all admissable attacks. (Consider unstable $A$ for non-trivial.)

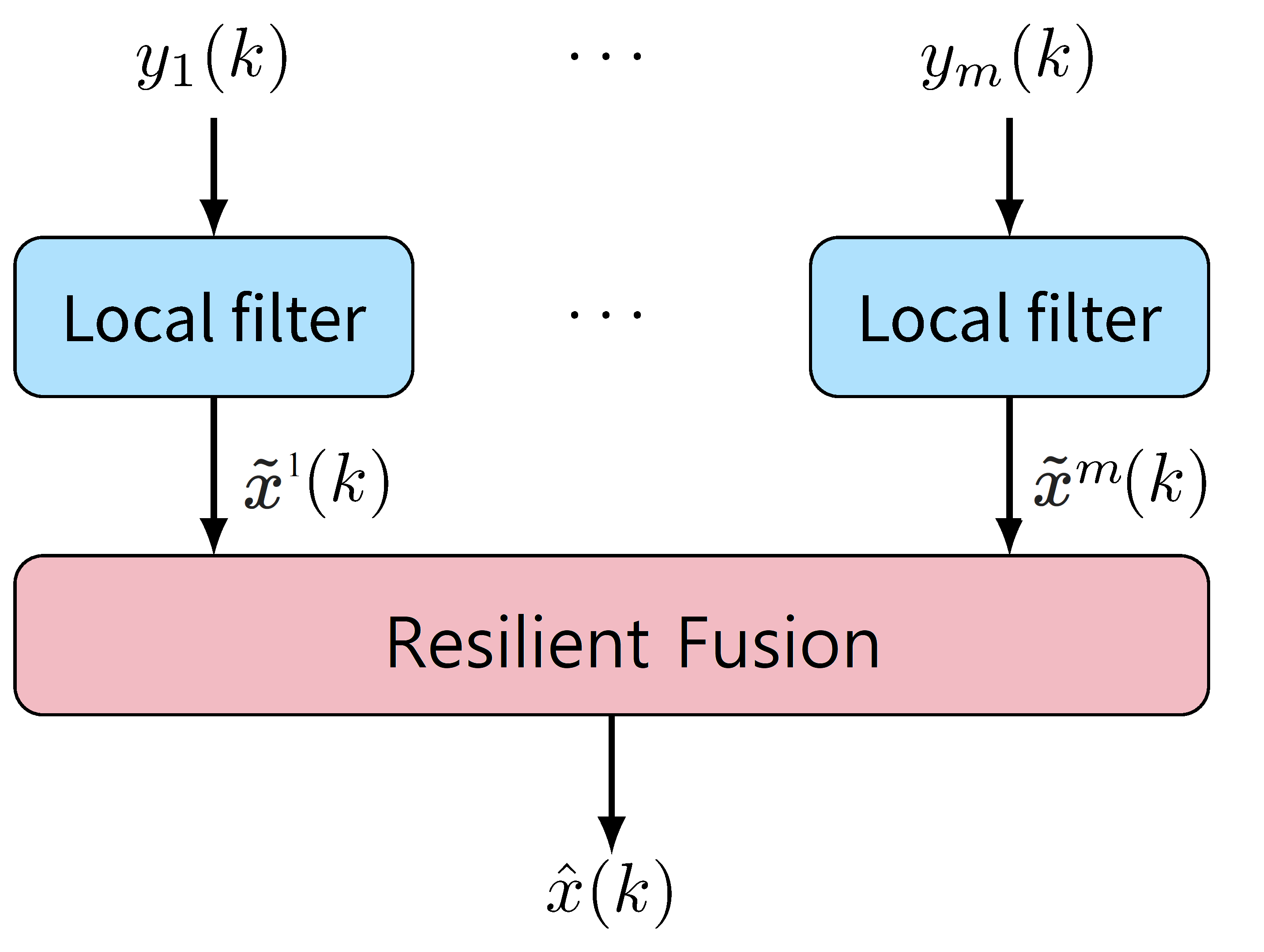
Decomposition-Fusion

Preliminaries on Local Observable Subspace Decomposition

$$A=\begin{bmatrix} \lambda_1 &0\\ 0&\lambda_2 \end{bmatrix}, \quad C=\begin{bmatrix} 1 &0\\ 0&1\\ 1 &1\\ 1&2 \end{bmatrix}.$$
  • Define that the observable space w.r.t. sensor $i$ as $$\mathbb{O}_i\triangleq {\rm span} \{C_i^\top , (C_i A)^\top, \cdots, (C_i A^{n-1})^\top \}.$$
  • We find that $\mathbb{O}_1={\rm span}\{e_1\}, \mathbb{O}_2={\rm span}\{e_2\},\mathbb{O}_3={\rm span}\{e_1, e_2\}, \mathbb{O}_4={\rm span}\{e_1, e_2\} $, where
    $$e_1\triangleq \begin{bmatrix}1& 0\end{bmatrix}^\top , e_2\triangleq \begin{bmatrix}0& 1\end{bmatrix}^\top $$

    • Preliminaries on Local Observable Subspace Decomposition

    $$A=\begin{bmatrix} \lambda_1 &0\\ 0&\lambda_2 \end{bmatrix}, \quad C=\begin{bmatrix} 1 &0\\ 0&1\\ 1 &1\\ 1&2 \end{bmatrix}.$$
    We find:
  • Sensor 1 can observe state entry 1.
  • Sensor 2 can observe state entry 2.
  • Sensor 3 can observe state entry 1,2.
  • Sensor 4 can observe state entry 1,2.
    • There are only 4 observability possibilities for one sensor:
    (1) Can observe no entry. (2) Can observe entry 1.
    (3) Can observe entry 2. (4) Can observe entry 1,2.

    Preliminaries on Local Observable Subspace Decomposition

    Assumption 1

    All the eigenvalues of matrix $A$ have geometric multiplicity 1.

    Theorem 1

    If Assumption 1 holds, the observable space of a sensor has a group of canonical basis vector. Thus, a sensor either can observe a state entry or not.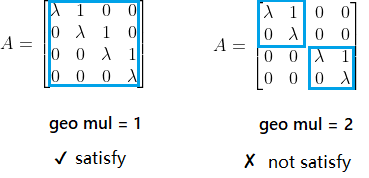

    [1]Mao, Y., Mitra, A., Sundaram, S., and Tabuada, P. (2022). On the computational complexity of the secure state-reconstruction problem. Automatica, 136, 110083.

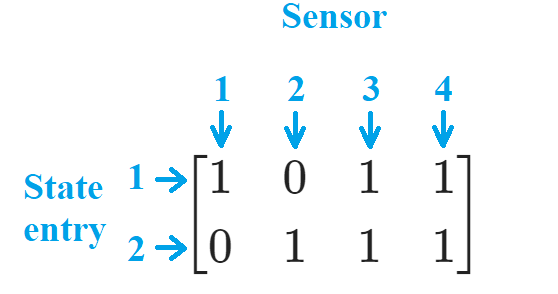
    Define the observability relationship matrix $\mathcal{Q}$ is constructed by $$ [\mathcal{Q}]_{i,j}=\begin{cases} 0, e_j\notin \mathbb{O}_i\\ 1, e_j\in \mathbb{O}_i \end{cases}.\qquad $$
    Define sensor $i$'s reduced-order subsystem as $(\tilde{A_i}, \tilde{C_i})$, it is observable. (linear system with $n_i$ states, 1 sensor)

    Local Observable Subspace

    $$A=\begin{bmatrix} \lambda_1 &0\\ 0&\lambda_2 \end{bmatrix}, \quad C=\begin{bmatrix} 1 &0\\ 0&1\\ 1 &1\\ 1&2 \end{bmatrix}.$$ The observability relationship is recorded in a 0-1 Matrix $\mathcal{Q}$: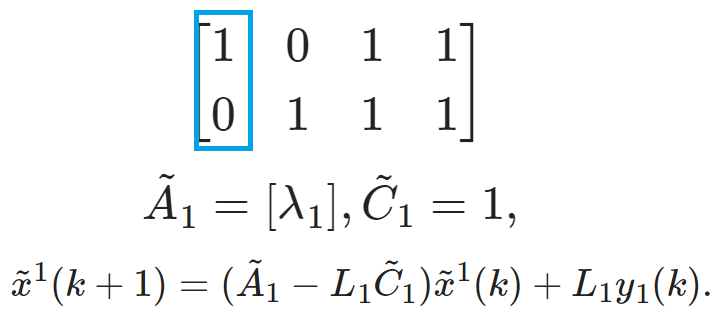

    Local Observable Subspace

    $$A=\begin{bmatrix} \lambda_1 &0\\ 0&\lambda_2 \end{bmatrix}, \quad C=\begin{bmatrix} 1 &0\\ 0&1\\ 1 &1\\ 1&2 \end{bmatrix}.$$ The observability relationship is recorded in a 0-1 Matrix $\mathcal{Q}$: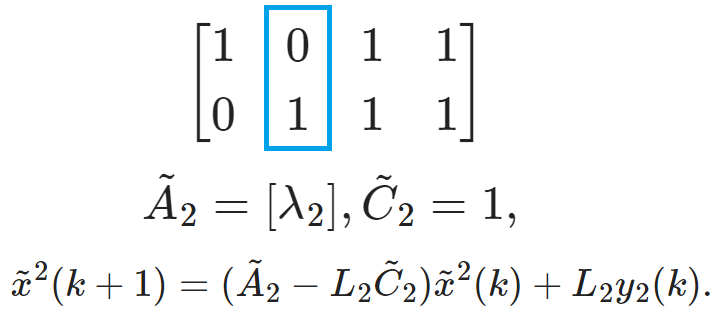

    Local Observable Subspace

    $$A=\begin{bmatrix} \lambda_1 &0\\ 0&\lambda_2 \end{bmatrix}, \quad C=\begin{bmatrix} 1 &0\\ 0&1\\ 1 &1\\ 1&2 \end{bmatrix}.$$ The observability relationship is recorded in a 0-1 Matrix $\mathcal{Q}$: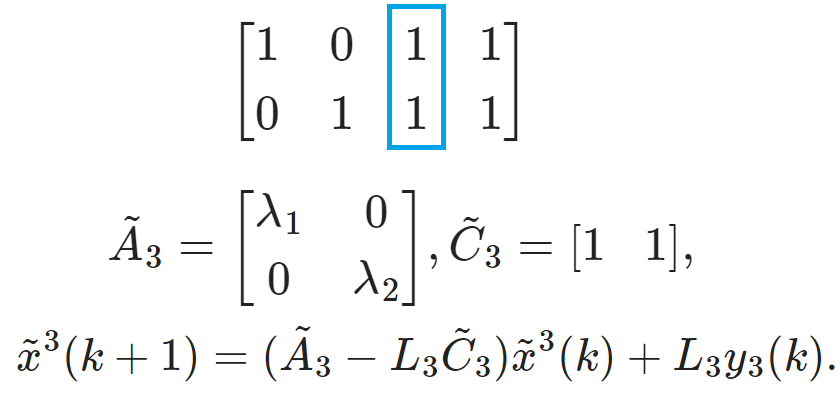

    Local Observable Subspace

    $$A=\begin{bmatrix} \lambda_1 &0\\ 0&\lambda_2 \end{bmatrix}, \quad C=\begin{bmatrix} 1 &0\\ 0&1\\ 1 &1\\ 1&2 \end{bmatrix}.$$ The observability relationship is recorded in a 0-1 Matrix $\mathcal{Q}$: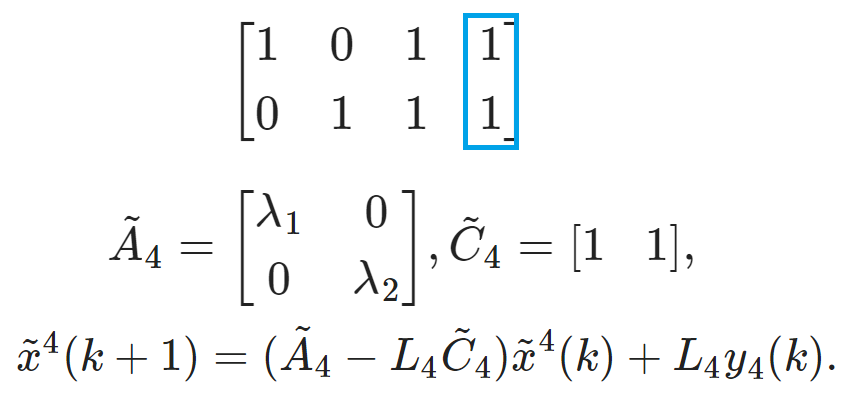

    Example on Resilient Fusion

    For 4 local observer states: $$\tilde{x}^1\in\mathbb{R}^1, \tilde{x}^2\in\mathbb{R}^2, \tilde{x}^3\in\mathbb{R}^1, \tilde{x}^4\in\mathbb{R}^2 $$
    Fuse those subsystems by taking median:

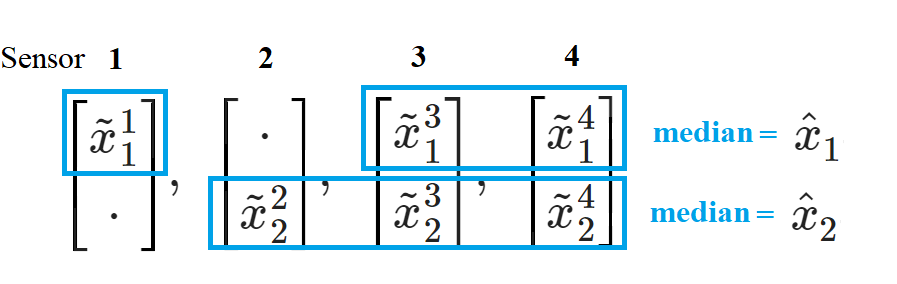
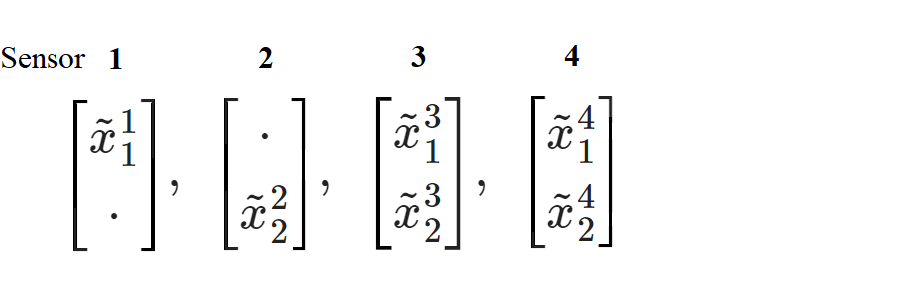
    Secure Estimation Algorithm against static sparse attack

    Lemma 1

    If the system is $2p$ sparse observable, then $\hat{x}(k)$ above has uniformly bounded error under static sparse attack where ${\rm supp} \{a(k)\}\subset \mathcal{C}$.
    $$ \|\hat{x}(k)-x(k)\|_\infty\leq {\rm Constant}\qquad \qquad \qquad \quad$$

    $2p$ sparse observable: System is still observable after removing arbitrary $2p$ sensors.

    Secure Estimation Algorithm against static sparse attack

    Lemma 1

    If the system is $2p$ sparse observable, then $\hat{x}(k)$ above has uniformly bounded error under static sparse attack where ${\rm supp} \{a(k)\}\subset \mathcal{C}$.
    $$ \|\hat{x}(k)-x(k)\|_\infty\leq {\rm Constant}(\mathcal{B}_w,\mathcal{B}_v,A,C,L_i) $$

    $2p$ sparse observable: System is still observable after removing arbitrary $2p$ sensors.

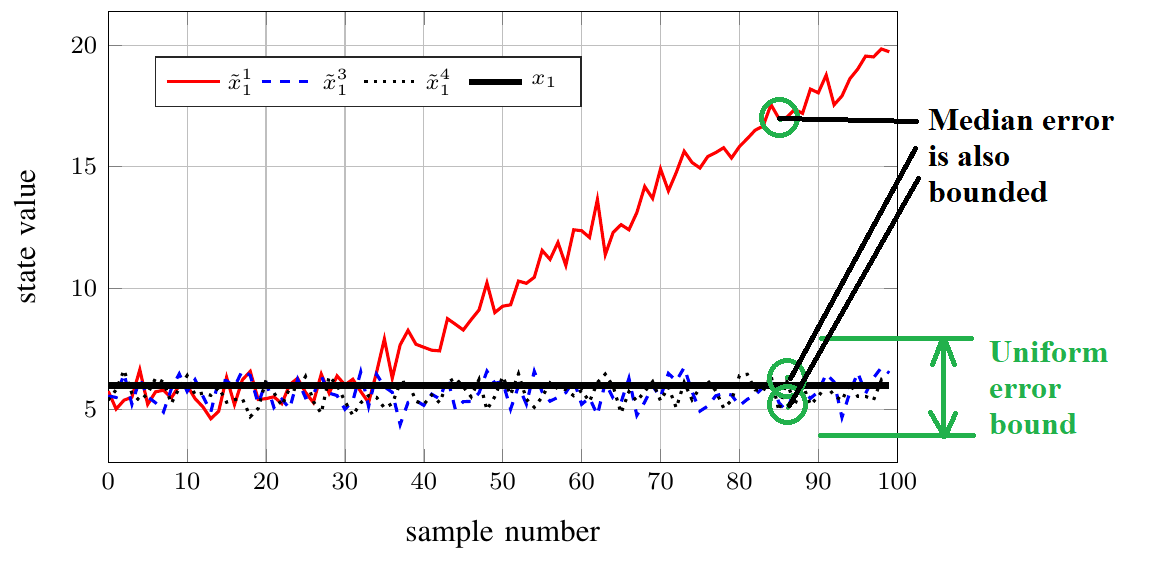
    Result under attack on fixed set

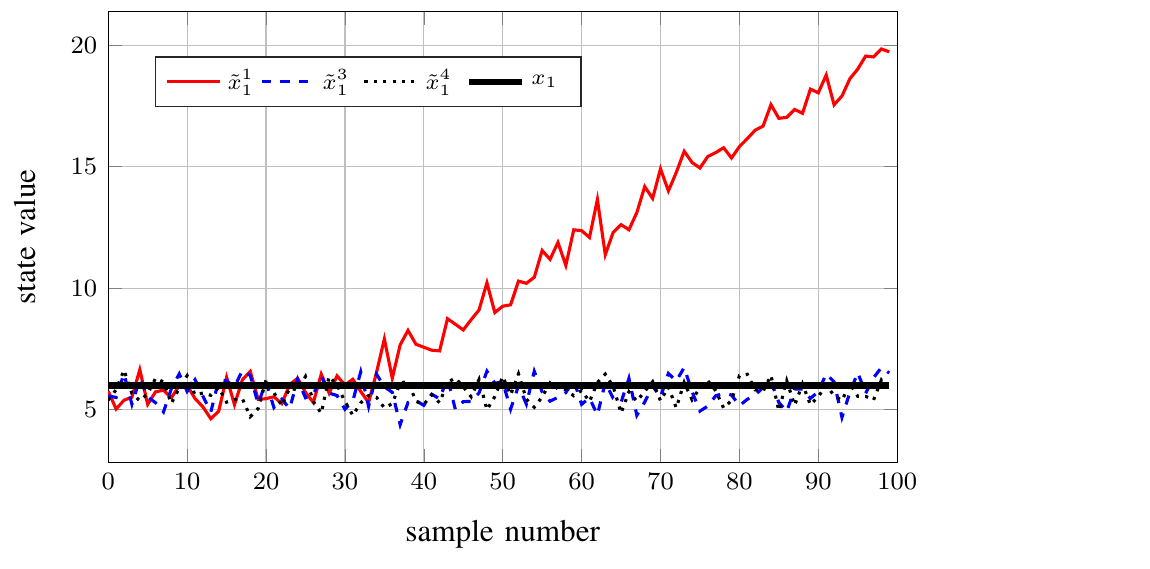
    Result under attack on fixed set

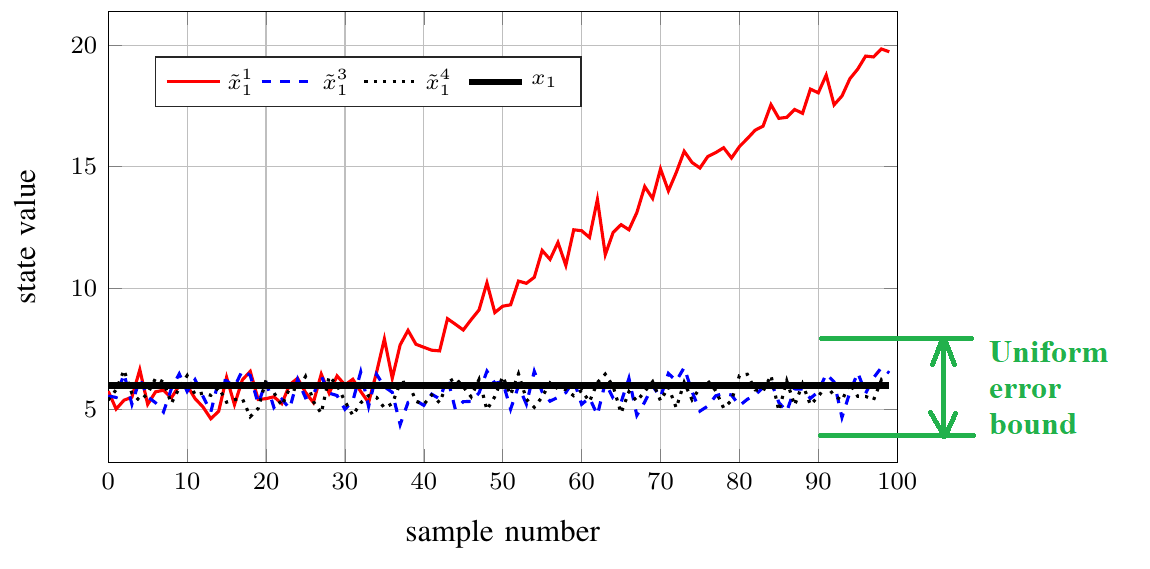
    Result under attack on fixed set

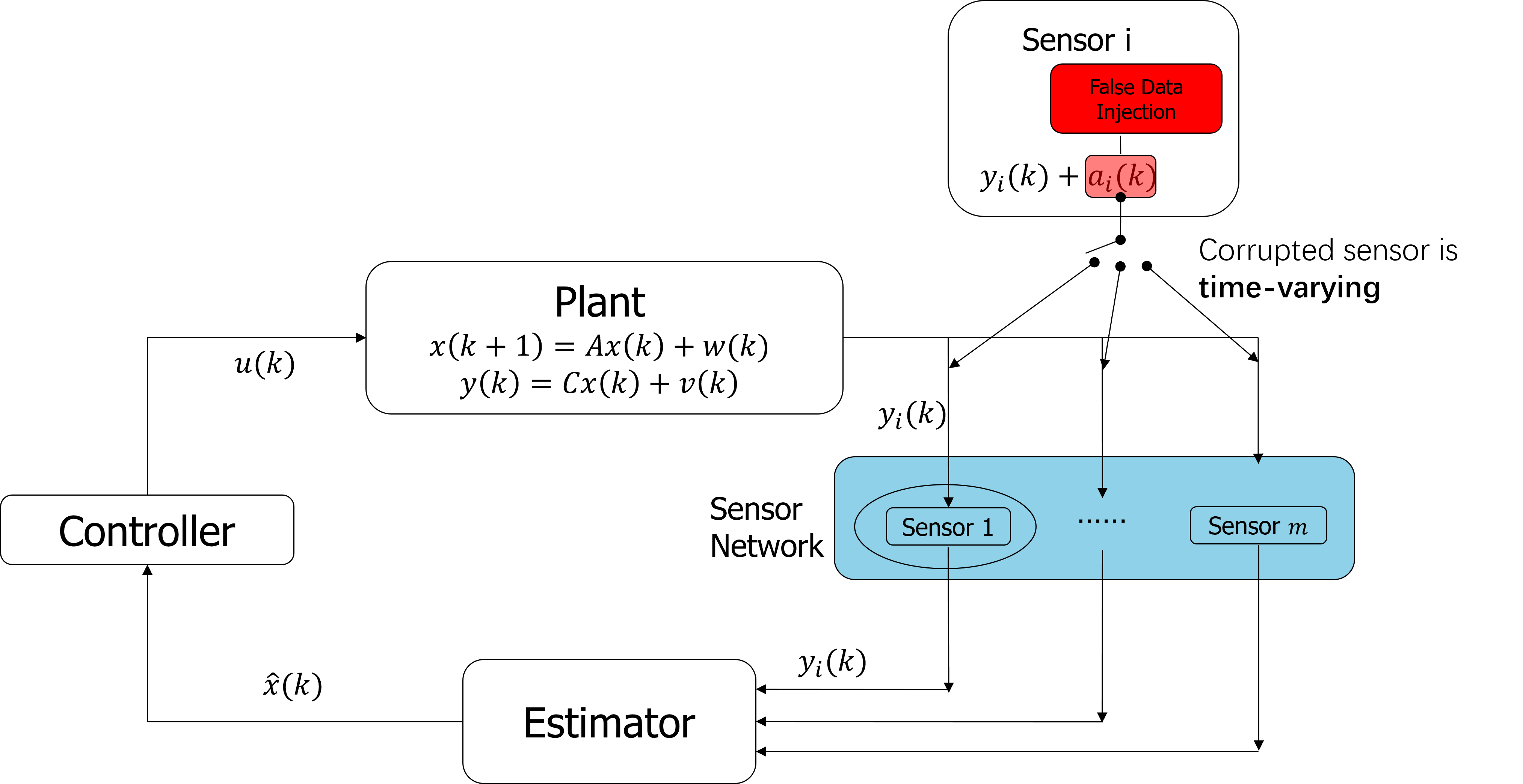
    What about time-varying corrupted sensor set?

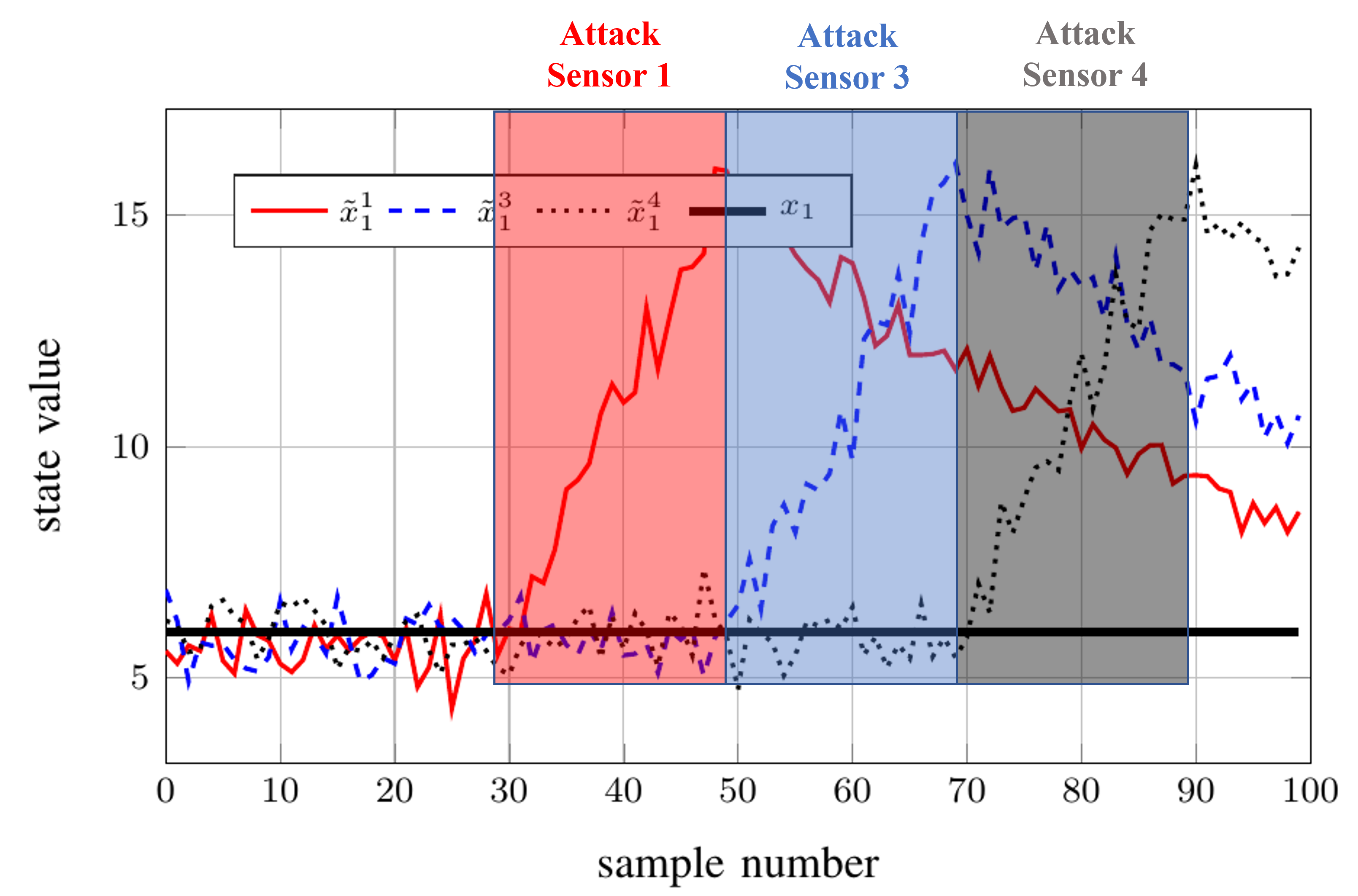
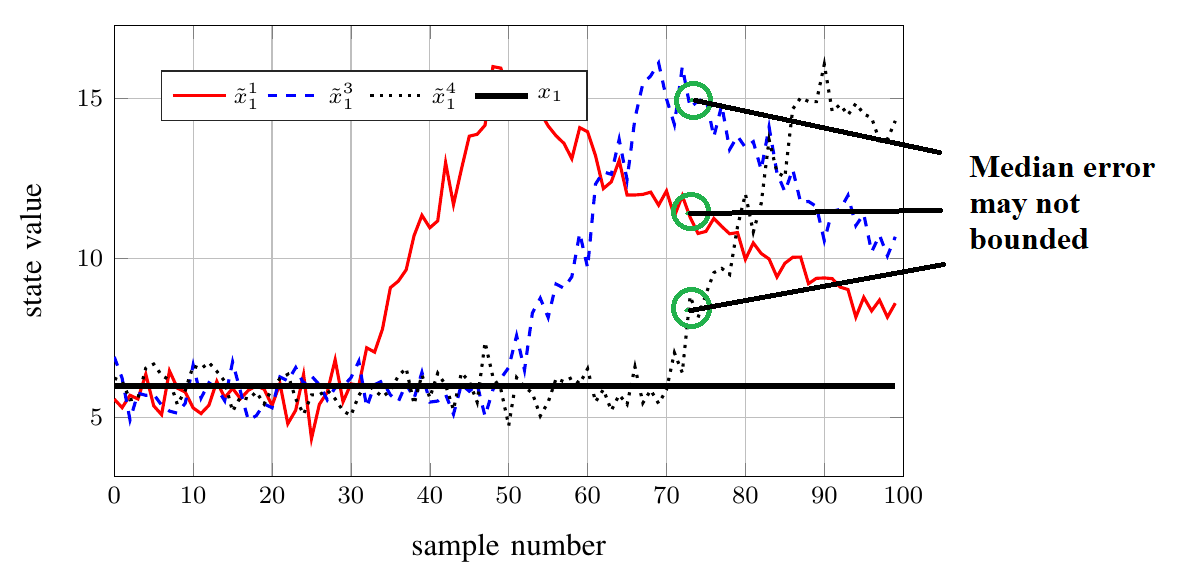
    What about time-varying corrupted sensor set?

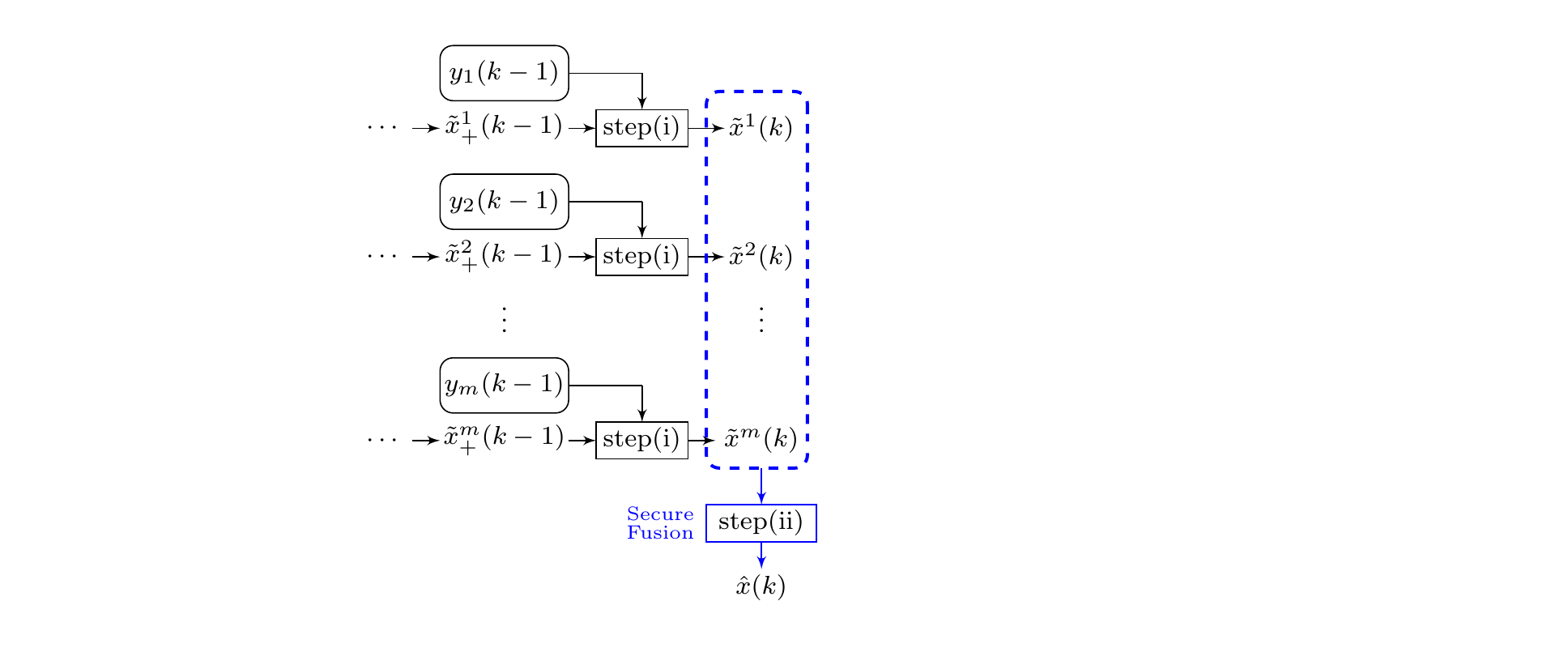
    Secure Estimation Algorithm

    Step 1: update local observer state. $$\tilde{x}^i(k+1)=(\tilde{A}_i - L_i \tilde{C} ) \tilde{x}^i_+ (k)+L_i y_i(k)$$

    Secure Estimation Algorithm

    Step 2: For each state entry, take median among all local states that can observe them.

    Secure Estimation Algorithm

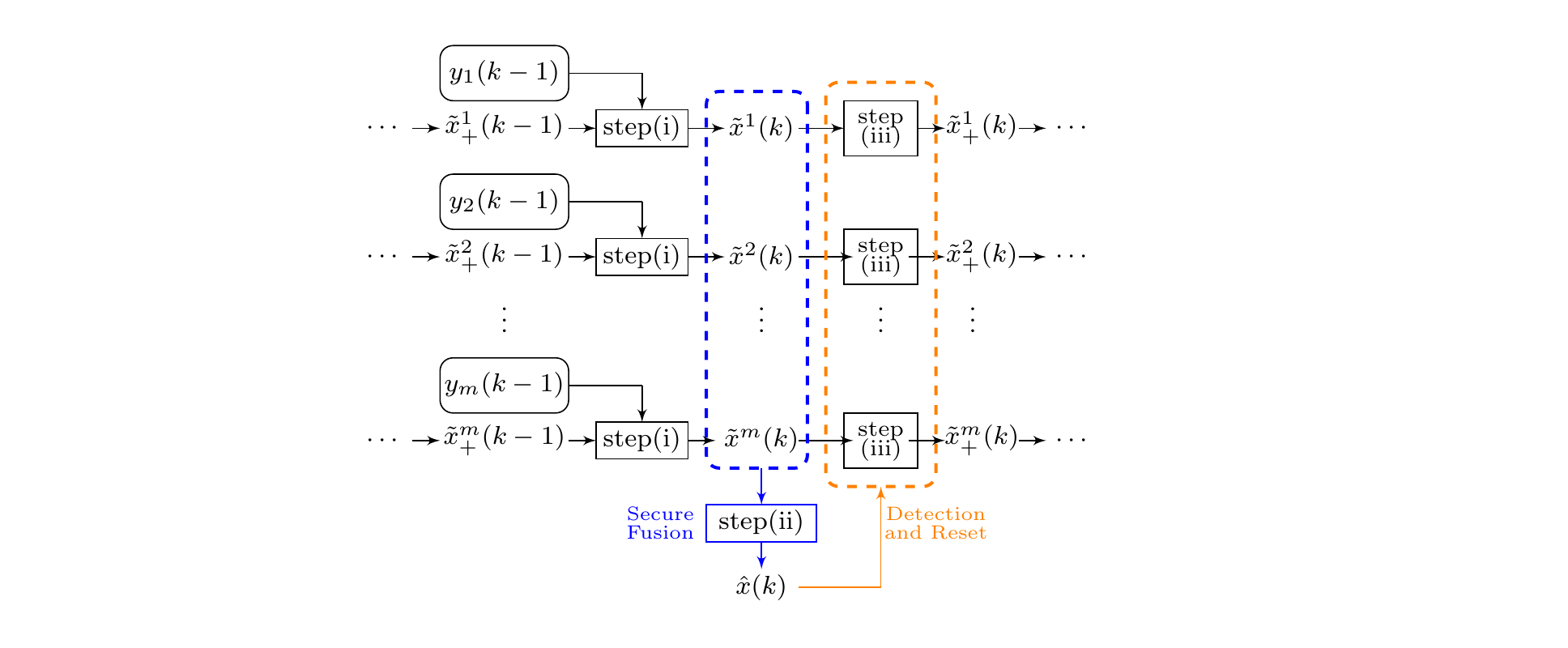
    Step 3: Check compatibility of all those local estimates for each sensor $i$, state entry $j$:
    $$ \tilde{x}^i_j:= \begin{cases} \tilde{x}^i_j, \text{ if } \|\tilde{x}^i-\hat{x}\|_2\leq (\sqrt{n_i}+1)\gamma \quad \textcolor{blue}{\rm (keeps\ the\ same) }\\ \hat{x}_j, \text{ if } \|\tilde{x}^i-\hat{x}\|_2> (\sqrt{n_i}+1)\gamma \quad \textcolor{red}{\rm (reset) } \end{cases} $$

    Main result on secure estimation (Theorem 2)

    Assume the system is $2p$-sparse observable and the following two conditions hold:
    (1) $\sigma_{\max}\left(\tilde{A}_i-L_i\tilde{C}_i\right)\leq \frac{1}{2\sqrt{n_i}+1}$, $i=1,2,\cdots,m$.
    (2) The initial estimate satisfies $\|\hat{x}(0)-x(0)\|_\infty\leq \gamma$.
    Then our algorithm provides a secure state estimate $\hat{x}$ in the sense that $$\|\hat{x}(k)-x(k)\|_\infty \leq \gamma,\quad \forall k\in\mathbb{Z}^+.$$

    Remark on observability requirements

    $2p$-sparse observability
  • System is still observable after removing arbitrary $s$ sensors.
    • $1$ step $2p$-sparse observability
  • $C$ is still full column rank after removing arbitrary $s$ sensors.
    • Where is the fundamental limit?

    [2]Nakahira, Y. and Mo, Y. (2018). Attack-resilient H2, H$\infty$, and $\ell 1$ state estimator. IEEE Transactions on Automatic Control, 63(12), 4353–4360.

    [3]X. He, X. Ren, H. Sandberg and K. H. Johansson, "How to Secure Distributed Filters Under Sensor Attacks," in IEEE Transactions on Automatic Control, vol. 67, no. 6, pp. 2843-2856.

    Remark on observability requirements

    Ours observability condition
  • $2p$-sparse observable
  • $\min_{L_i} \sigma_{\max}(\tilde{A}_i-L_i\tilde{C}_i)<\frac{1}{2\sqrt{n_i}+1},\ i=1,2,\cdots,m$

    • [2]Nakahira, Y. and Mo, Y. (2018). Attack-resilient H2, H$\infty$, and $\ell 1$ state estimator. IEEE Transactions on Automatic Control, 63(12), 4353–4360.

    [3]X. He, X. Ren, H. Sandberg and K. H. Johansson, "How to Secure Distributed Filters Under Sensor Attacks," in IEEE Transactions on Automatic Control, vol. 67, no. 6, pp. 2843-2856.

    Remark on the error bound

    $\|\hat{x}(0)-x(0)\|_{\infty}\leq \gamma \Rightarrow \|\hat{x}(k)-x(k)\|_{\infty}\leq \gamma$

    Theoretical Perspective

    The result is non-trivial when the system is unstable

    Practical Perspective

    The initial time $k=0$ is seen as the time when the attack is launched and operator switch from a classic estimator to our algorihtm.

    Simulation on IEEE 14 bus system

  • generator bus $\mathcal{V}_g=\{1,2,3,6,8\}$, load bus $\mathcal{V}_l=\{2,3,4,5,6,9,10,11,12,13,14\}$
  • $14\times 2=28$ states (phase angle, angle velocity)
  • $14\times 4=56$ measurements (phase angle$\times 2$, angle velocity, electric power)
    • $$ \dot{\theta}_{i}(t) =\omega_{i}(t), $$ $$\dot{\omega}_{i}(t) =-\frac{1}{m_{i}}\left[D_{i} \omega_{i}(t)+\sum_{j \in \mathcal{N}_{i}} P_{t i e}^{i j}(t)- P_{i}(t)+w_{i}(t)\right].$$
    $$ \left[\begin{array}{ccc} y_{i_1}(k) & y_{i_2}(k) & y_{i_3}(k)& y_{i_4}(k) \end{array}\right]^\top=\left[\begin{array}{ccc} P_{e l e c, i}(k) & \theta_{i}(k)& \omega_{i}(k) & \omega_{i}(k) \end{array}\right]^{\top}+v_{i}(k), $$

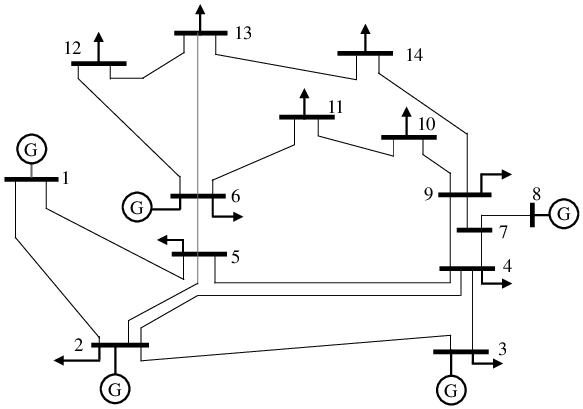
    Attack set design

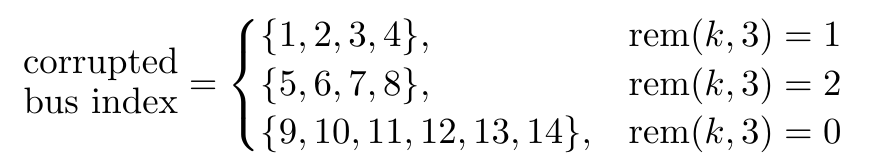
    The attack set loops for every 3 time steps.

    Random signal attack

    $a_i(k)$ is a random value uniformly distributed in interval $[-10,10]$.

    Slope signal attack

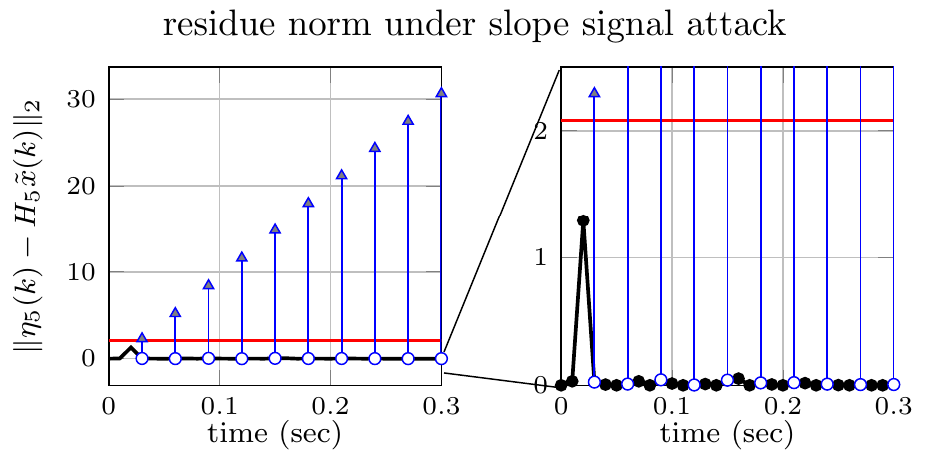
    $a_i(k)=k/5$ i.e., the magnitude of injected data increases 20 for every second.

    Random signal attack

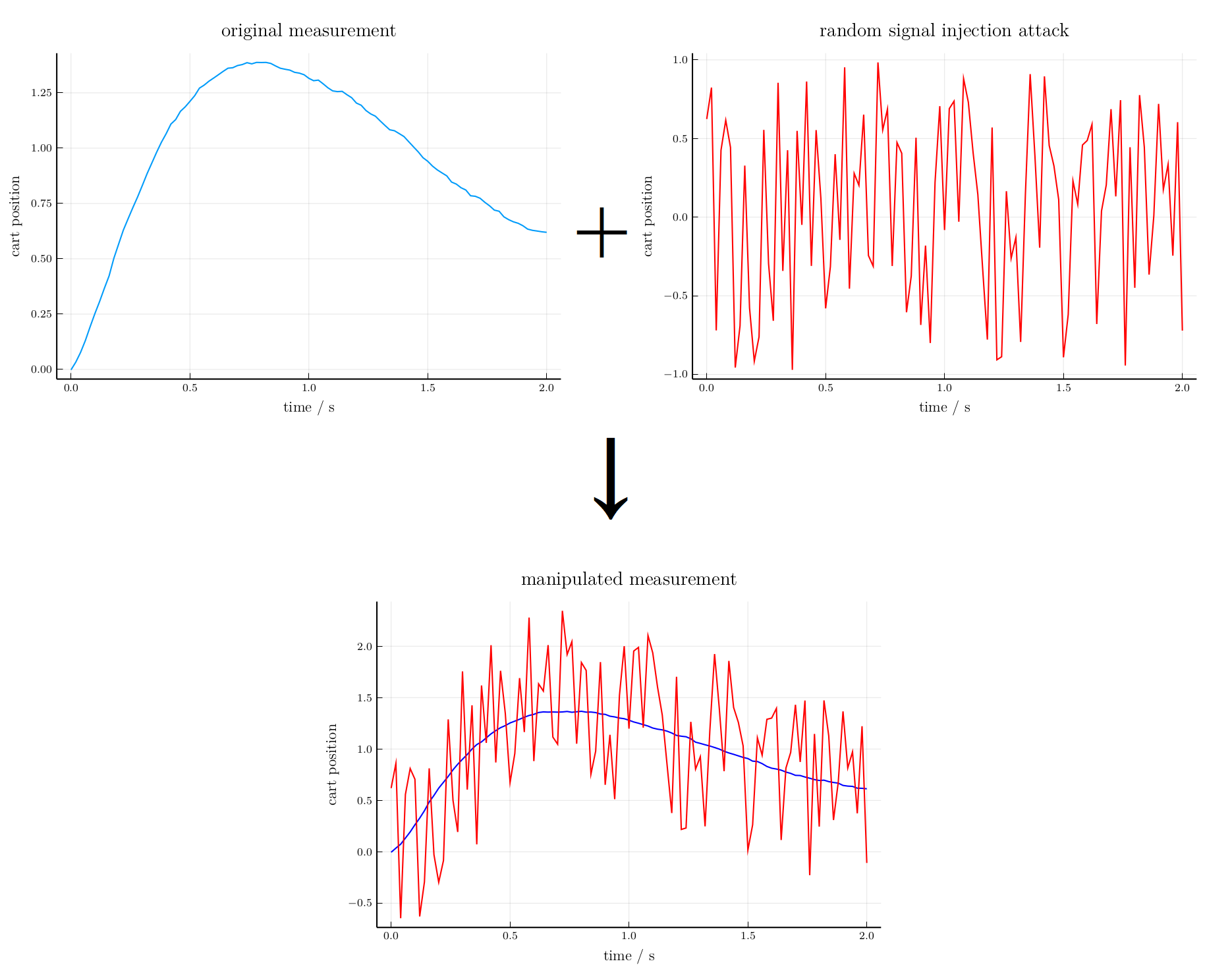
    Figure

    Estimation performance under random attack signal

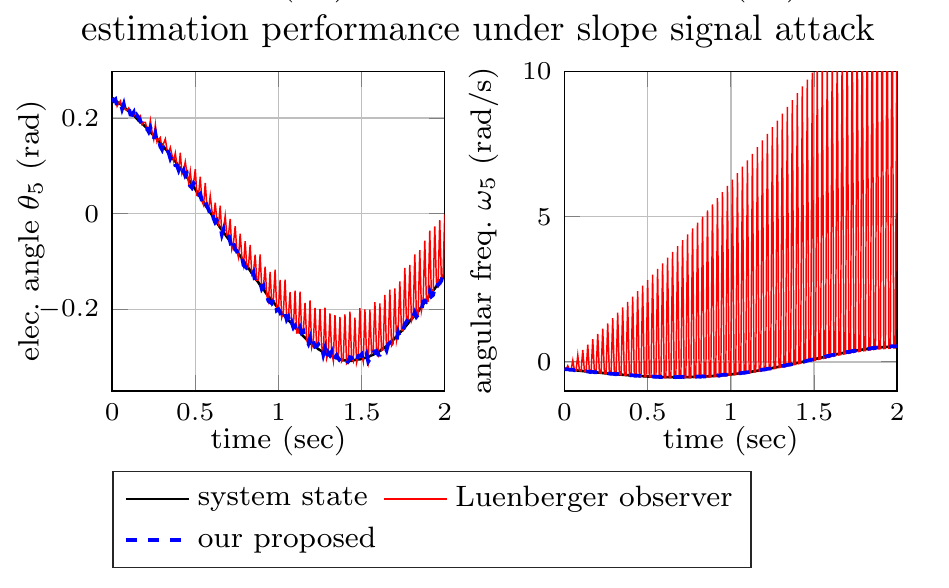
    Figure

    Slope signal attack

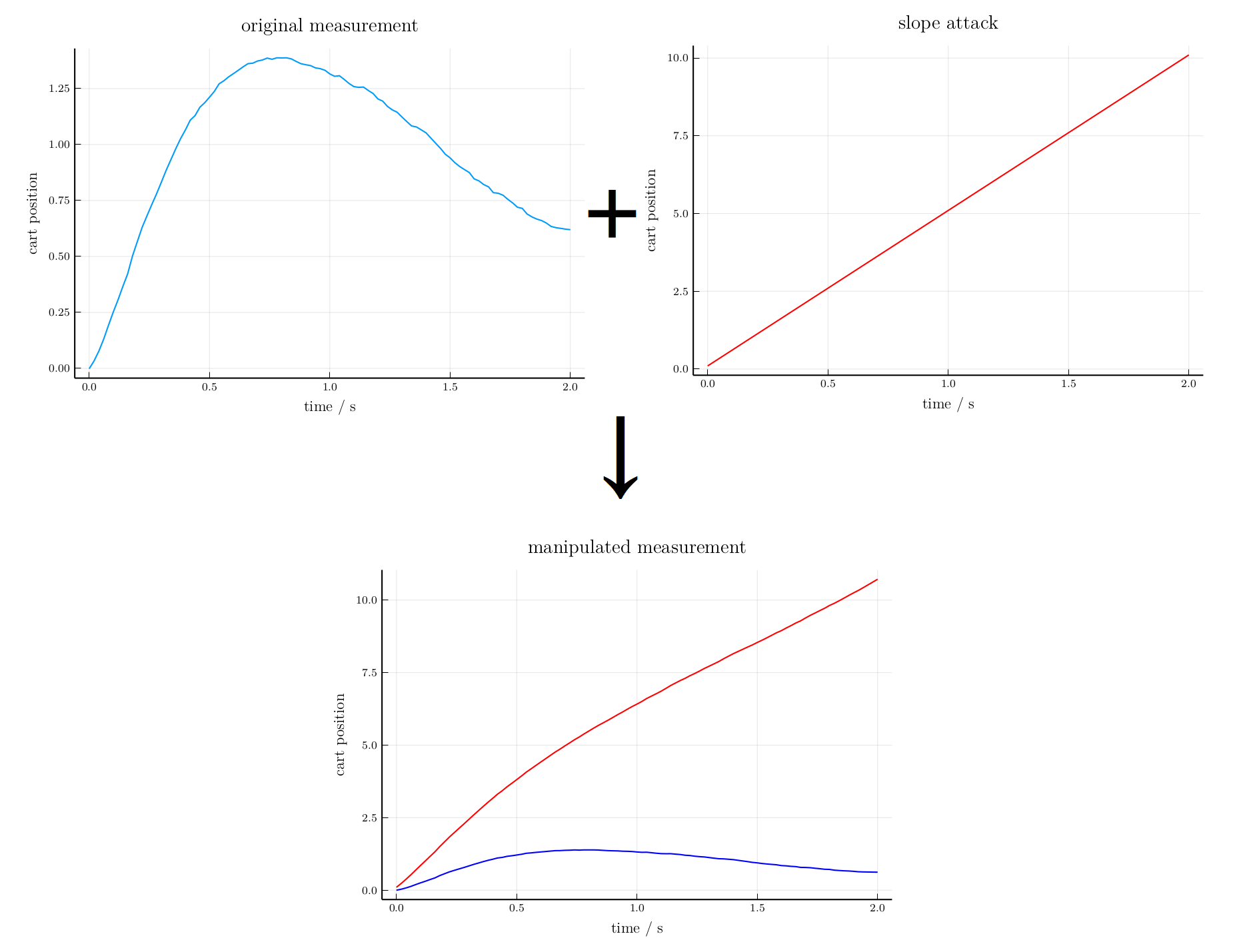
    Figure

    Estimation performance under slope attack signal

    Figure

    Residue decrease by resetting

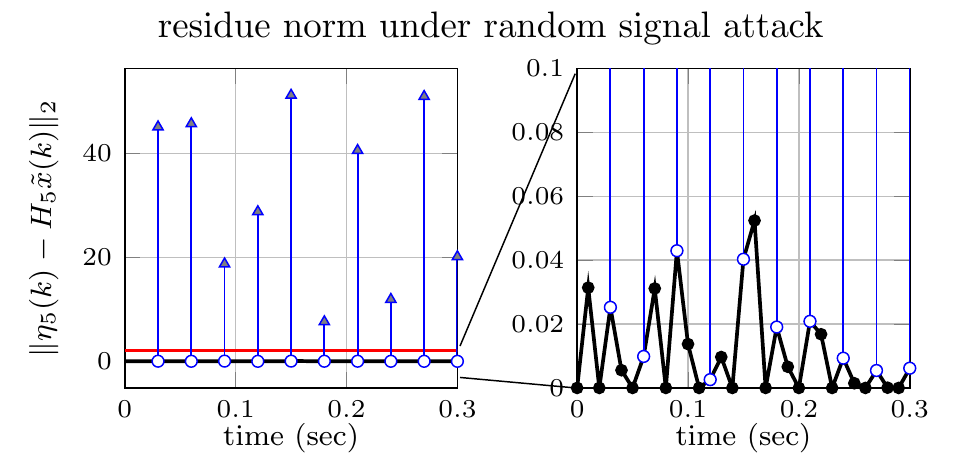
    Residue decrease by resetting

    Summary

    Propose an algorithm for time-varying $p$-sparse attack on sensors.
    Algorithm structure
  • Step 1: local observer update
  • Step 2: median fusion
  • Step 3: Detection and reset
    • Requirements
  • Condition on observability (closer to fundamental limit)
  • Non-derogatory dynamic matrix $A$
    • Results
  • secure estimation $\|\hat{x}(k)-x(k)\|_\infty\leq \gamma$.
  • No false alarm.

    • The slides can be seen at

    https://zs-li.github.io/talk/IFAC2023/index.html

    Figure

    My e-mail is:

    lizs19@mails.tsinghua.edu.cn

    Questions from the audience!